Exemples d'utilisation d'IMAGEO

Voici plusieurs exemples d'activités utilisant Imageo et destinées à des élèves de collège.

  1. Le cercle circonscrit au triangle

    2. Cette activité a été la première activité menée avec IMAGEO par une classe de 5ème. Elle avait trois objectifs : apprendre à utiliser IMAGEO, rappeler la construction du centre du cercle circonscrit à un triangle et ensuite étudier la position de ce centre en fonction de la forme du triangle. Elle a été menée en une heure avec des groupes de 14 élèves en salle informatique. Chaque élève disposait ainsi d'un ordinateur.

    Construction de la figure

    Pendant cette phase toute la classe avance au même rythme. On commence en lançant l'éditeur associé à IMAGEO, puis en ouvrant une feuille vierge. Après avoir brièvement expliqué le principe du programme, le professeur dicte certaines lignes du programme de construction de la figure, en faisant les commentaires appropriés, et laisse les élèves écrire celles qui seront similaires. A chaque fois qu'une ligne est écrite on lance IMAGEO pour vérifier que le programme est bien compris, cela permet de repérer rapidement les fautes d'orthographe ou les erreurs de syntaxe. La première fois il faut donner un nom au fichier de travail : un mot formé par un maximum de 8 lettres sans caractères accentués et sans espaces. L'éditeur ajoutera automatiquement l'extension .FIG.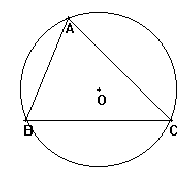

    Programme de construction

    
'création des 3 sommets du triangle
A=POINT(-2,3)
B=POINT(-4,-2)
C=POINT(3,-2)
'création des 3 côtés du triangle
AB=SEGMENT(A,B)
BC=SEGMENT(B,C)
AC=SEGMENT(C,A)
'construction de 2 médiatrices
I=MILIEU(A,B)
J=MILIEU(B,C)
D1=PERPENDICULAIRE(AB,I)
D2=PERPENDICULAIRE(BC,J)
'construction du cercle
O=INTERSECTION(D1,D2)
C0=CERCLE(O,A)
'ne montrer que les éléments de l'énoncé
CACHER(I,J,D1,D2)

    Exploitation de la figure

    Toute la classe a obtenu à l'écran un triangle ABC et son cercle circonscrit de centre O. En modifiant la position des points A, B et C on voit le cercle changer de centre et de rayon. On peut alors étudier les deux questions suivantes.
    Existence du cercle
    Trouver une position des points A, B et C pour laquelle il n'y a pas de cercle circonscrit. Justifier.
    Les élèves découvrent vite que le cercle disparait lorsque les points A, B et C sont alignés. On peut alors essayer de trouver une explication à cette disparition : les deux médiatrices tracées étant parallèles, le point d'intersection n'existe pas.
    Position du centre
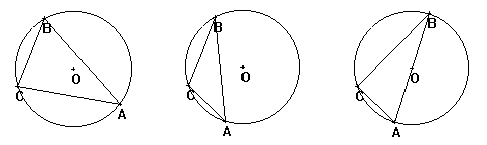
    Le centre du cercle circonscrit se trouve parfois à l'intérieur et parfois à l'extérieur du triangle. Quel rapport y a-t-il entre sa position et la forme du triangle ?
    Le but est de faire découvrir que le centre se trouve à l'extérieur du triangle lorsque celui-ci a un angle obtus et à l'intérieur lorsqu'il a 3 angles aigus. On peut alors se poser le problème du cas limite: un angle est à la fois aigu et obtus ou le centre se trouve à la fois à l'intérieur et à l'extérieur. La propriété du triangle rectangle d'admettre le milieu de l'hypoténuse comme centre du cercle circonscrit arrive ainsi de façon très naturelle.

    Activité complémentaire

    Si le temps restant est suffisant, on peut terminer l'heure en faisant construire les 3 médianes, puis les trois hauteurs du triangle et étudier la position du centre de gravité et de l'orthocentre.

  2. Les parallélogrammes

    3. Cette activité permet de revoir la construction d'un parallélogramme à partir de 3 points, puis de mettre en évidence les parallélogrammes particuliers. Elle a été menée en une heure avec une classe de cinquième qui avait déjà utilisé IMAGEO

    Construction du parallélogramme

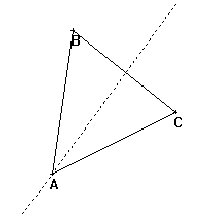
    L'énoncé donné oralement à la classe est : on se donne trois points A,B et C, il faut construire le point D tel que ABCD soit un parallélogramme. Les élèves doivent écrire le programme de construction. Plusieurs méthodes de construction peuvent être utilisées. Chacune fait appel à une propriété caractéristique différente du parallélogramme.
    Partie commune
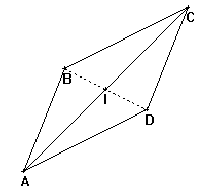
    Tous les programmes de construction auront une partie commune qui consiste à dessiner le triangle ABC, puis à dessiner les côtés CD et DA du parallélogramme, ainsi que sa diagonale BD. 
    
'création des points A, B et C
A=POINT(-4,-3)
B=POINT(-2,2)
C=POINT(3,4)
'création des côtés du triangle
AB=Segment(A,B)
AC=Segment(A,C)
BC=Segment(B,C)
'construction du point D
...
...
...
'dessin du parallélogramme
CD=SEGMENT(C,D)
DA=SEGMENT(D,A)
BD=SEGMENT(B,D)
POINTILLE(B,D)
    Méthode 1
    Les côtés opposés d'un parallélogramme sont parallèles. On construit donc un quadrilatère ABCD qui a cette propriété. 
    
'construction du point D
D1=PARALLELE(AB,C)
D2=PARALLELE(BC,A)
D=INTERSECTION(D1,D2)
'mise en forme
CACHER(D1,D2)
    Le programme fonctionnant bien, on pourra admettre qu'un quadrilatère qui a des côtés opposés parallèles est un parallélogramme. On pourra toutefois remarquer que le triangle ABC doit être un vrai triangle, c'est à dire que ses sommets ne doivent pas être alignés.
    Méthode 2
    Les diagonales d'un parallélogramme se coupent en leur milieu. On construit un quadrilatère ABCD qui a cette propriété. 
    
'construction du point D
I=Milieu(A,C)
D=Symétrique(B,I)
    Le programme fonctionnant bien, on pourra admettre qu'un quadrilatère dont les diagonales se coupent en leur milieu est un parallélogramme. Cette façon de procéder n'admet aucune restriction.
    Méthode 3
    Deux côtés opposés d'un parallélogramme ont même longueur. On construit un quadrilatère ABCD qui a cette propriété. 
    
'construction du point D
C1=CERCLE(C,AB)
C2=CERCLE(A,BC)
'il faut choisir un des deux points d'intersection
D=INTERSECTION((C1,C2,2)
'mise en forme
CACHER(C1,C2)
    Cette fois-ci, le programme de construction a une petite faiblesse. Le point D a été construit comme intersection de deux cercles, or celle-ci contient en général deux points. Il a fallu choisir l'un des deux et en modifiant la position des points A, B et C on se rend compte que celui qui a été désigné n'est pas toujours le bon. On admettra cette fois qu'un quadrilatère non croisé qui a des côtés opposés de même longueur est un parallélogramme.
    Méthode 4
    La quatrième méthode reprend la pratique habituelle sur papier quadrillé : on construit un quadrilatère ABCD qui a deux côtés opposés de même longueur. 
    
'construction du point D
D1=PARALLELE(BC,A)
C1=CERCLE(A,BC)
'il faut choisir un des deux points d'intersection
D=INTERSECTION(D1,C1,1)
'mise en forme
CACHER(D1,C1)
    Encore une fois le programme de construction a une petite faiblesse. Le point D a été construit comme intersection d'une droite et d'un cercle, or celle-ci contient en général deux points. Il a fallu choisir l'un des deux et en modifiant la position des points A, B et C on se rend compte que celui qui a été désigné n'est pas toujours le bon. On admettra cette fois qu'un quadrilatère non croisé qui a deux côtés opposés de même longueur est un parallélogramme.

    Premières conclusions

    Pendant cette activité les propriétés du parallélogramme sont apparues comme de véritables outils servant à définir une stratégie de construction. D'autre part, les restrictions qui interviennent dans les deux dernières méthodes ont été découvertes par les élèves pendant les manipulations et non parachutées par le professeur qui a envie de faire preuve de rigueur.

    Etude des parallélogrammes particuliers

    On utilise le parallélogramme obtenu avec la 2ème méthode (utilisation du centre de symétrie) et on commence par faire remarquer les 'évidences' suivantes : Ces remarques étant faites, les questions suivantes sont posées :
    Comment faut-il choisir les points A, B et C pour que ABCD soit : Les élèves doivent déplacer les points A,B et C pour obtenir les configurations demandées et être en mesure de répondre. Ils ont de plus ainsi l'occasion de constater concrètement qu'un losange est un parallélogramme ou qu'un carré est un losange.

    Activité complémentaire

    On pourra aussi proposer l'énoncé voisin suivant :
    ABC est un triangle, D et E sont les symétriques de B et C par rapport à A.
    1) Quelle est la nature du quadrilatère BCDE ?
    2) Quelle doit être la particularité de ABC pour que BCDE soit :
    - un losange ?
    - un rectangle ?
    - un carré ?

  3. Bissectrice d'un angle

    4. La construction de la bissectrice d'un angle à la règle et au compas est devenue une opération tellement classique qu'on oublie souvent de se demander pourquoi elle fonctionne si bien. Cette activité, destinée à des élèves de 6ème ou de 5ème, essaie de les amener à répondre à cette question.

    L'hypothèse de départ

    On dessine un triangle ABC et on essaie de construire la bissectrice de l'angle BAC. Il y a toujours un élève pour proposer de dessiner la droite passant par A et le milieu de BC et un autre pour expliquer une histoire d'arcs de cercles. La première proposition étant plus simple et plus compréhensible est en général bien acceptée par la classe. On décide donc de la mettre en oeuvre et on observe en déplaçant les 3 sommets.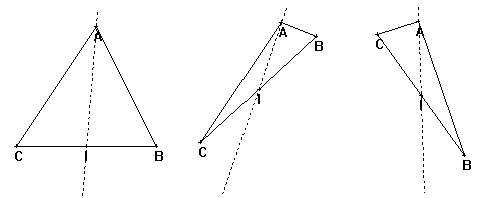

    Si la figure de départ peut laisser penser que la proposition était bonne, on se rend vite compte que ce n'est pas le cas en déplaçant les points B et C. C'est une bonne occasion de dire que la droite tracée s'appelle médiane. On peut de plus constater que lorsque AB diminue, l'angle BAI devient nettement plus grand que CAI et que c'est le contraire qui se produit lorsque AC diminue.
    Avant d'abandonner l'idée proposée qui a semblé si évidente on va chercher dans quelles conditions elle peut se révéler exacte. La réponse ne tarde pas, il faut que le triangle ABC soit isocèle, son axe de symétrie permet d'expliquer facilement cette propriété.

    Utilisation de la constatation précédente

    Dessiner la bissectrice de l'angle principal d'un triangle isocèle est donc facile. Comment se débrouiller avec un triangle quelconque ? En lui adjoignant un triangle isocèle ! Il suffira de choisir un point E sur (AB) et un point F sur (AC) tels que AE=AF. La bissectrice de EAF passe par A et le milieu de EF, mais comme l'angle EAF est aussi l'angle BAC on aura obtenu la bissectrice de BAC.
    Les points E et F seront construits en traçant un cercle de centre A et en prenant son intersection avec AB et AC.
    On obtient le programme de construction suivant: 
    
'points A, B et C
A=Point(-1,-3)
B=Point(0,4)
C=Point(5,0)
Polygone(A,B,C)
DAB=Droite(A,B)
DAC=Droite(A,C)
'points E et F
Ce=Cercle(A,5)
E=Intersection(DAB,Ce,1)
F=Intersection(DAC,Ce,1)
'bissectrice
I=Milieu(E,F)
Bis=Droite(A,I)
Pointillé(BIS)
    qui fournit la figure suivante :
    En ajoutant la ligne Cacher(DAB,DAC,E,F,I,Ce), on obtient une figure débarrassée des traits de construction.

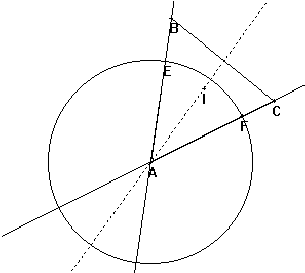
    Un cas particulier gênant

    La manipulation de la figure précédente peut faire apparaître une situation particulière : lorsque le points A est sur le segment BC la bissectrice disparaît, alors qu'elle devrait être la perpendiculaire à (BC) passant par A. En se souvenant que la bissectrice est définie comme la droite passant par les points A et I, on se rend compte que dans le cas particulier qui nous intéresse ces deux points sont confondus, ce qui explique l'impossibilité de tracer la droite.
    Pour résoudre le problème posé par ce cas particulier, on revient au triangle isocèle AEF et on essaie de définir la bissectrice de EAF d'une autre façon. C'est la droite passant par A et I, mais aussi la hauteur issue de A ou la médiatrice de BC. Ceci nous donne deux nouvelles méthodes de construction pour lesquelles le problème ne se pose plus.

    Retour au papier et au crayon

    Après cette activité, la méthode classique de construction d'une bissectrice à la règle et au compas aura un peu perdu de son caractère magique, l'élève qui avait raconté une histoire d'arcs de cercles sera en mesure de retrouver le sens de son histoire, des mathématiques seront passées par là.

  4. Symétrie axiale

    5. IMAGEO possède des fonctions qui permettent de construire facilement le symétrique d'un point par rapport à une droite ou par rapport à un point. Cela permet d'envisager une façon intéressante de présenter ces notions.
    Dans un premier temps on peut construire un triangle et son symétrique. La possibilité de modifier le triangle ou de changer la position de l'axe ou du centre de la symétrie permet de l'étudier de manière globale. Les propriétés qui sont conservées (distances, angles, ...) ainsi que celles qui ne le sont pas (orientation) apparaissent de façon assez évidente. Les élèves sont en mesure d'émettre des hypothèses et de tester leur validité.
    Dans un deuxième temps on pourra se limiter à la figure formée par un point unique et son symétrique et chercher à découvrir les propriétés géométriques qui lient ces deux points et qui permettront de les construire sans recourir à la fonction SYMETRIQUE d'IMAGEO.
    En classe de troisième on pourra procéder de même pour étudier la composition des symétries : étude globale pour conjecturer un résultat, étude sur un point pour en chercher la démonstration.

    Symétrie axiale en 6ème

    On crée un triangle ABC et un axe qui sera défini par deux points E et F, puis on construit le symétrique de ABC par rapport à l'axe. Ceci nous donne le programme de construction suivant : 
    
E=Point(0,5)
F=Point(0,-5)
Axe=Droite(E,F)
A=Point(-6,2)
B=Point(-8,-2)
C=Point(-2,-1)
A1=Symétrique(A,Axe)
B1=Symétrique(B,Axe)
C1=Symétrique(C,Axe)
Polygone(A,B,C)
Polygone(A1,B1,C1)
    et la figure associée :

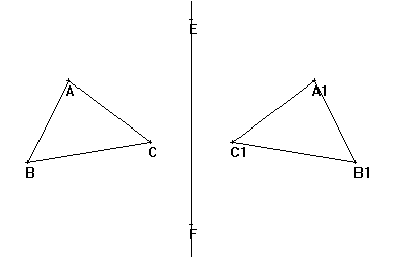
    L'axe a été volontairement choisi vertical pour obtenir une figure conforme à la représentation de la symétrie que les élèves ont déjà. On pourra dans un premier temps empêcher le déplacement de cet axe en fixant la position de E et F grâce à l'instruction FIXER(E,F).
    L'observation de la figure initiale mène à des conclusions classiques sur la conservation des distances. La modification de la position des points A, B et C va permettre d'effectuer d'autres constatations, en particulier sur la position d'un point et de son symétrique par rapport à l'axe. On pourra aussi faire apparaître les droites AB et A1B1 et observer la propriété de leur point d'intersection.

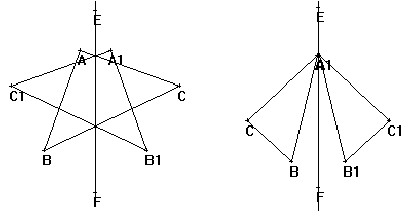
    Tant que l'axe de la symétrie est vertical, les remarques des élèves font souvent intervenir les notions de droite et de gauche. On va alors pouvoir libérer les points E et F et modifier la position de l'axe de symétrie.

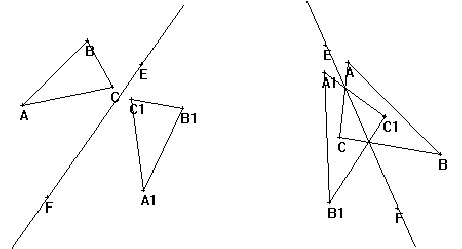
    Les notions de droite, gauche, haut ou bas pourront alors être remplacées par la notion de demi-plan. De nouvelles images de la symétrie ont pu naitre.
    Ce qu'IMAGEO a réalisé simplement avec sa fonction SYMETRIQUE, il faudra être capable de le faire sur papier. Pour cela il faut découvrir le secret de ces figures. On pourra se limiter au cas du point A et de son symétrique A1. En dessinant le segment qui joint ces deux points on suscitera des hypothèses : l'axe est perpendiculaire au segment AA1 et passe par son milieu. Ces hypothèses seront d'abord vérifiées en déplaçant les points A, E et F. Une expérience pourra être imaginée pour les confirmer : dessiner un segment AB, la droite perpendiculaire à ce segment en son milieu puis le point A1 symétrique de A par rapport à cette droite. C'est le fait que B et A1 soient confondus qui confirmera l'hypothèse.
    Introduire une expérience dans un cours de mathématiques peut sembler quelque peu hérétique. Les mathématiques ne sont pas une science expérimentale. Que cette expérience serve à justifier une définition est tout aussi bizarre, on justifie les propriétés et non les définitions qui sont données a priori ! Ceci est sans doute exact lorsqu'on se propose d'exposer des mathématiques, mais le but était ici de permettre aux élèves d'en construire, donc de se placer avant l'exposé. Les expériences ont à ce moment un rôle important à jouer en donnant du sens à l'exposé futur et en évitant que celui-ci apparaisse comme une vérité révélée issue des textes sacrés dont le professeur est le dépositaire.

  5. Lieu d'un point

    6. Enoncé

    On considère un cercle de centre O et un point fixe A.
    A chaque point P du cercle on associe le point M milieu de [AP].
    Etudier le lieu du point M lorsque P décrit le cercle.

    Construction de la figure

    
'définition des éléments de la figure
O=Point(0,0)
C=Cercle(O,5)
A=Point(2,3)
P=PointSur(C,a=100)
M=Milieu(A,P)
'interdire la modification de O et A
Fixer(O,A)
'conserver la trace de M
Trace(M)

    Utilisation

    Le seul élément mobile de la figure est le point P attaché au cercle. En déplaçant le point P, on provoque un déplacement du point M qui laisse une trace.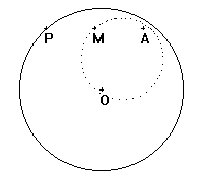

    Celle-ci correspond à un cercle.
    Le problème est alors de définir ce cercle en donnant son centre et son rayon. On pourra laisser les élèves faire des propositions de point et construire ces points. Enfin le dessin du triangle POA et du milieu I de [OA] laissera entrevoir une démonstration possible.
Voir aussi :