L'interface de YFX
L'écran est divisé en 2 parties :- sur la gauche se trouve une série de boutons permettant d'envoyer des commandes;
- sur la droite se trouve la zone de données qui contient les représentations graphiques ou les tableaux de valeurs.
Boutons de commande
Les boutons de commandes sont :| Y= | pour définir les fonctions à étudier. |
| CONFIG | pour définir les paramètres utilisés pour les représentations graphiques et les tableaux de valeurs. |
| TABLE | permet de passer en mode tableau de valeurs. |
| COURBE | permet de passer en mode représentation graphique. |
| MENU | donne accès à des commandes spéciales |
| AIDE | pour afficher le fichier d'aide en ligne. |
| QUITTER | permet de quitter le programme. |
Définition des fonctions étudiées
Appuyer sur le bouton Y= permet de définir les 4 fonctions à étudier.Une boîte de dialogue permet de remplir les champs Y1, Y2, Y3 et Y4 qui correspondent aux quatre fonctions.
Certains de ces champs peuvent rester vides.
La définition d'une fonction f(x) peut utiliser les opérations (+, - , * , / et ^) ainsi que des parenthèses sur plusieurs niveaux.
Le symbole * de la multiplication peut être omis s'il ne se trouve pas entre deux lettres.
Le symbole ² représente la fonction carré.
L'expression PI représente le nombre pi.
Les fonctions suivantes sont définies :
| FRAC | partie fractionnaire |
| ENT | partie entière |
| ABS | valeur absolue |
| RAC | racine carrée |
| CAR | carré |
| SIN | sinus |
| COS | cosinus |
| TAN | tangente |
| ARCSIN | arc sinus |
| ARCCOS | arc cosinus |
| ARCTAN | arc tangente |
| ARGSH | argument sinus hyperbolique |
| ARGCH | argument cosinus hyperbolique |
| ARGTH | argument tangente hyperbolique |
| EXP | exponentielle |
| LN | logarithme népérien |
| LOG | logarithme décimal |
| SH | sinus hyperbolique |
| CH | cosinus hyperbolique |
| TH | tangente hyperbolique |
En mode Courbe
Utilisation de la souris- appuyer sur le bouton gauche permet de tracer des lignes de rappel vers les axes de coordonnées
- appuyer sur le bouton droit permet d'afficher les coordonnées du point visé
- les touches fléchées permettent de déplacer l'origine du repère
- les touches Page Haut et Page Bas permettent d'agrandir ou de diminuer la fenêtre de visualisation des courbes
En mode Table
- Les touches Flèche Haut et Flèche Bas permettent de modifier la valeur de départ de la table.
- Les touches Page Haut et Page Bas permettent de modifier le pas de calcul entre deux valeurs
Configuration du mode Courbe
Appuyer sur le bouton Configurer permet de définir les caractéristiques du repère utilisé pour la représentation graphique.Une boîte de dialogue permet de remplir les champs :
| Xmin | valeur minimale de x |
| Xmax | valeur maximale de x |
| Xgrad | pas de graduation de l'axe des x |
| Ymin | valeur minimale de y |
| Ymax | valeur maximale de y |
| Ygrad | pas de graduation de l'axe des y |
Configuration du mode Table
Appuyer sur le bouton Configurer permet de définir les caractéristiques du tableau de valeurs.Une boîte de dialogue permet de remplir les champs :
| Xdep | valeur initiale de x |
| Pas | différence entre deux valeurs successives de x |
Utilisation du menu
Le menu permet de sauvegarder :- l'image des courbes tracées dans un fichier au format PCX
- les données d'un tableau de valeurs dans un fichier texte.
Attention : l'impression des courbes n'est possible que sur des imprimantes compatibles Epson ou IBM Proprinter.
Thèmes d'utilisation de YFX
La possibilité de tracer des courbes définies par des équations du type y=f(x) pourra être exploitée en 4ème ou en 3ème dans différents contextes.Equations de droites
On pourra facilement mettre en évidence le rôle des paramètres a et b dans l'équation y=ax+b d'une droite en traçant de nombreuses droites de façon simultanée. En se limitant aux droites d'équations y=ax on fera apparaître les relations entre a et la direction de la droite, ce qui justifiera la dénomination "coefficient directeur". En fixant la valeur de a et en faisant varier b on remarquera que les droites de même coefficient directeur sont parallèles (on passe de l'une à l'autre par une translation) et on pourra donner un sens à l'expression "ordonnée à l'origine" utilisée pour nommer b.
Equations et inéquations du premier degré
La solution d'une équation du type ax+b=cx+d peut être obtenue avec le point d'intersection des droites y=ax+b et y=cx+d. On peut relier le problème de l'existence de solutions avec la position relative des deux droites. D'autre part la relation entre équation et inéquation apparaît de façon assez claire.
Equations non linéaires
Les problèmes donnant lieu à des équations non linéaires permettent souvent de vraies activités de recherche car les élèves ne disposent pas de méthodes toutes faites pour les résoudre. Qu'il s'agisse de résoudre une équation, de rechercher un maximum ou un minimum la construction de graphiques et surtout leur interprétation sera toujours une phase intéressante.
Tracé de la courbe y=x².
On commence par tracer la courbe y=x². Il suffit pour cela d'appuyer sur le bouton "Tracer" et d'entrer x² ou x*x dans la ligne d'édition de la boîte de dialogue qui apparaît.On valide avec la touche Entrée et la courbe se trace immédiatement.
Pour permettre à chacun de comprendre la signification de cette courbe, on peut commencer par vérifier qu'elle passe bien par les points de coordonnées (n, n²) avec n entier relatif. Il suffit de montrer ces points avec la souris et d'appuyer sur le bouton droit. Ce faisant on pourra remarquer facilement que les carrés sont toujours positifs et que le fait que deux nombres opposés ont le même carré se traduit par l'existence d'un axe de symétrie.
Equation x²=a
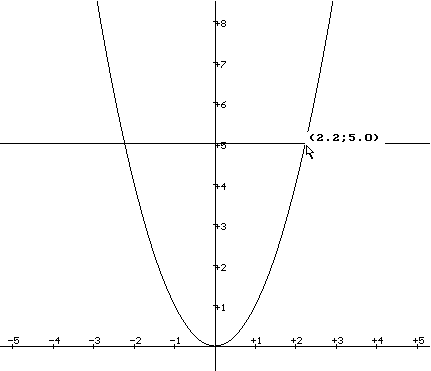
On se propose ensuite de résoudre l'équation x²=5.Les élèves pourront commencer par chercher une solution en faisant glisser la souris le long de la courbe. Il sera aussi intéressant de faire tracer la droite y=5.
Cette droite permet de placer correctement la souris de façon immédiate. Mais elle nous montre aussi qu'il existe deux solutions qui correspondent d'ailleurs à des points symétriques. On appellera racine carrée de 5 la solution positive.
Le programme indique 2.2 comme valeur de la racine de 5. On peut vérifier rapidement qu'il s'agit d'une valeur approchée. Pour obtenir une approximation plus précise on peut utiliser le bouton "Loupe" et agrandir la partie du plan qui entoure le point intéressant. En recommençant plusieurs fois cette opération on peut obtenir trois décimales.
On revient à la figure de départ en appuyant sur le bouton "Rétablir" et on se demande si ce que l'on a observé s'applique à d'autres valeurs que 5. La figure permet de voir rapidement que l'équation x²=a n'a de solutions que si a est positif; lorsqu'on trace une droite d'équation y=a avec a négatif, elle ne coupe pas la courbe y=x². On pourra aussi noter le rôle de 0 qui correspond à un point de l'axe de symétrie; comme ce point est son propre symétrique, il correspond à une solution 'double'.
La courbe y=rac(x)
On efface la courbe y=x² (en utilisant le bouton "Effacer") et on trace la courbe d'équation y=rac(x); "rac" signifie racine carrée pour le programme.On peut immédiatement observer que la courbe n'occupe que la partie droite de l'écran, les nombres négatifs n'ont pas de racine carrée.
La forme de la courbe obtenue rappelle celle qu'on avait auparavant avec y=x². On trace de nouveau la courbe y=x² pour avoir les deux courbes simultanément à l'écran. On constate alors une symétrie entre la courbe y=rac(x) et une partie de la courbe y=x². On peut même tracer l'axe de cette symétrie en remarquant qu'il s'agit de la droite y=x.
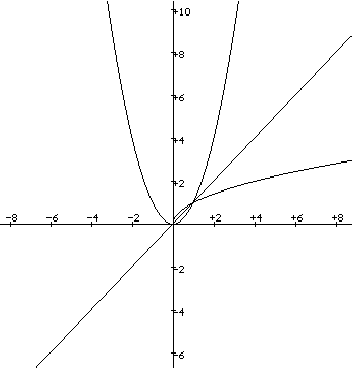
Comment comprendre l'existence de cet axe de symétrie ? La symétrie entre les relations y=x² et x=rac(y) constitue un élément d'explication, surtout si l'on a déjà remarqué que la symétrie par rapport à la droite y=x s'obtient en inversant le rôle de l'abscisse et de l'ordonnée.
On pourra enfin profiter du graphique obtenu pour étudier des équations et des inéquations du type x²=x ou rac(x)>x.