Utiliser un Tableur en classe

Voici quelques exemples d'utilisation d'un tableur pour proposer des activités mathématiques à des élèves de collège.

  1. Le jeu TIC TAC

    2. L'idée de cette activité est issue du manuel de 4ème de la collection Pythagore. Elle a pour but de comparer croissance linéaire et croissance exponentielle. L'utilisation du tableur est justifiée par la quantité de calculs à effectuer tout en conservant une trace des résultats obtenus. D'autre part nous utiliserons ses capacités graphiques.

    La situation étudiée

    Le TIC TAC est un jeu télévisé qui propose de gagner une cagnotte. Celle-ci, qui contient 50F au départ va augmenter chaque minute. L'augmentation peut se faire de deux façons, elle est chaque minute Le problème est de comparer les 2 options et de choisir la meilleure.

    Construction de la feuille de calcul

    On commence par lancer TVTAB, puis on crée une feuille vierge en utilisant la commande Nouveau du menu Fichier.

    Etude de l'option A
    L'étude de l'option A se fait avec les élèves qui sont guidés pas à pas. Elle est l'occasion de présenter les principales notions qui permettent d'utiliser un tableur.

    Présentation
    On peut commencer par écrire un titre général de la feuille 'JEU DU TIC TAC' dans la cellule A1 et par le souligner dans la cellule A2.
    La cellule A4 contiendra le texte "OPTION A".
    A partir de la ligne 6 nous allons construire un tableau de 3 colonnes qui représenteront la durée écoulée, le montant de la cagnotte et le gain obtenu après une minute. On écrit les titres de ces colonnes: "Minutes" en A6, "Cagnotte" en B6 et "Gain" en C6.
    Colonne des minutes
    La colonne "Minutes" commence par 0 qu'on entre en A7. Sur la feuille apparaît 0.00. Les décimales sont inutiles pour cette colonne, on clique sur le A qui forme l'entête de la colonne pour la sélectionner entièrement, puis on applique la commande Format Cellule du menu Feuilles qui permet de choisir un affichage sans décimales.
    La cellule A8 doit contenir une unité supplémentaire, il suffira d'entrer la formule "=A7+1".
    Pour chacune des cellules qui se trouvent sous A8 il faut reproduire la même formule qui signifie 'prendre la valeur de la cellule supérieure et ajouter une unité'. On commence par Copier la cellule A8 en utilisant la commande Copier du menu Edition. On sélectionne ensuite les cellules A9:A67 et on appuie sur Entrée. La colonne se remplit de 1. La commande Recalcule du menu Feuilles permet de recalculer le tout et d'obtenir une suite d'entiers de 0 à 60 pour représenter les minutes.
    Colonne des gains
    La cellule C7 contient 100 car dans l'option A on gagne 100F chaque minute. Les cellules qui se trouvent dessous contiendront 100 aussi. On obtient ce résultat en effectuant un Copier/Coller comme pour les minutes.
    Colonne de la cagnotte
    La cellule B7 contient 50 qui est le montant initial de la cagnotte.
    La cellule B8 doit contenir le montant précédent de la cagnotte augmenté du gain. Cela se traduit par la formule "=B7+C7".
    Pour les cellules qui se trouvent dessous on doit indiquer une formule similaire, on utilise encore une fois un Copier/Coller.

    Etude de l'option B
    La construction du tableau correspondant à l'option B sera laissé à l'initiative des élèves qui auront ainsi l'occasion de mettre en pratique ce qu'ils auront appris.
    Ce tableau sera placé dans les colonnes E, F et G.
    La seule différence avec l'option A viendra de la colonne des gains qui ne sont plus constants. Il faudra écrire une première fois la formule calculant 10% de la cagnotte puis la copier dans les cases situées en dessous.

    Résultats obtenus

    Minutes Cagnotte A Gain A Minutes Cagnotte B Gain B
    0 50.00 100.00 0 50.00 5.00
    1 150.00 100.00 1 55.00 5.50
    2 250.00 100.00 2 60.50 6.05
    3 350.00 100.00 3 66.55 6.66
    4 450.00 100.00 4 73.21 7.32
    5 550.00 100.00 5 80.53 8.05
    6 650.00 100.00 6 88.58 8.86
    7 750.00 100.00 7 97.44 9.74
    8 850.00 100.00 8 107.18 10.72
    9 950.00 100.00 9 117.90 11.79
    10 1050.00 100.00 10 129.69 12.97
    11 1150.00 100.00 11 142.66 14.27
    12 1250.00 100.00 12 156.92 15.69
    13 1350.00 100.00 13 172.61 17.26
    14 1450.00 100.00 14 189.87 18.99
    15 1550.00 100.00 15 208.86 20.89
    16 1650.00 100.00 16 229.75 22.97
    17 1750.00 100.00 17 252.72 25.27
    18 1850.00 100.00 18 278.00 27.80
    19 1950.00 100.00 19 305.80 30.58
    20 2050.00 100.00 20 336.37 33.64
    21 2150.00 100.00 21 370.01 37.00
    22 2250.00 100.00 22 407.01 40.70
    23 2350.00 100.00 23 447.72 44.77
    24 2450.00 100.00 24 492.49 49.25
    25 2550.00 100.00 25 541.74 54.17
    26 2650.00 100.00 26 595.91 59.59
    27 2750.00 100.00 27 655.50 65.55
    28 2850.00 100.00 28 721.05 72.10
    29 2950.00 100.00 29 793.15 79.32
    30 3050.00 100.00 30 872.47 87.25
    31 3150.00 100.00 31 959.72 95.97
    32 3250.00 100.00 32 1055.69 105.57
    33 3350.00 100.00 33 1161.26 116.13
    34 3450.00 100.00 34 1277.38 127.74
    35 3550.00 100.00 35 1405.12 140.51
    36 3650.00 100.00 36 1545.63 154.56
    37 3750.00 100.00 37 1700.20 170.02
    38 3850.00 100.00 38 1870.22 187.02
    39 3950.00 100.00 39 2057.24 205.72
    40 4050.00 100.00 40 2262.96 226.30
    41 4150.00 100.00 41 2489.26 248.93
    42 4250.00 100.00 42 2738.18 273.82
    43 4350.00 100.00 43 3012.00 301.20
    44 4450.00 100.00 44 3313.20 331.32
    45 4550.00 100.00 45 3644.52 364.45
    46 4650.00 100.00 46 4008.98 400.90
    47 4750.00 100.00 47 4409.87 440.99
    48 4850.00 100.00 48 4850.86 485.09
    49 4950.00 100.00 49 5335.95 533.59
    50 5050.00 100.00 50 5869.54 586.95
    51 5150.00 100.00 51 6456.50 645.65
    52 5250.00 100.00 52 7102.15 710.21
    53 5350.00 100.00 53 7812.36 781.24
    54 5450.00 100.00 54 8593.60 859.36
    55 5550.00 100.00 55 9452.96 945.30
    56 5650.00 100.00 56 10398.25 1039.83
    57 5750.00 100.00 57 11438.08 1143.81
    58 5850.00 100.00 58 12581.89 1258.19
    59 5950.00 100.00 59 13840.07 1384.01
    60 6050.00 100.00 60 15224.08 1522.41

    Exploitation de la feuille de calcul

    La feuille de calcul étant réalisée, on l'utilise pour répondre au problème posé: quelle est la meilleure option ?

    Analyse des séries de nombres
    La comparaison des colonnes Cagnotte des deux options permet de constater que l'option A est nettement plus avantageuse au début mais qu'à partir d'un certain moment c'est l'option B qui l'emporte largement. On comprend ce phénomène en regardant les colonnes Gain des deux options. Les gains obtenus avec l'option B ne cessent d'augmenter car ils sont proportionnels à la cagnotte.

    Utilisation des graphiques
    En sélectionnant les colonnes Minutes et Cagnotte de l'option A et en utilisant la commande Points Reliés du menu Graphiques on obtient une représentation graphique de l'évolution de la cagnotte qui est une droite pour cette option. C'est la traduction de la constance du gain.
    La même opération pour l'option B nous donne un graphique de nature totalement différente, une courbe qui monte lentement au début et très vite à la fin. C'est la traduction de la croissance des gains.

    Traduction algébrique

    Il est possible pour terminer l'activité de donner une traduction algébrique des deux types d'évolution de la cagnotte en cherchant les formules appropriées. Le travail précédent sera alors utile à la compréhension des raisonnements permettant d'établir ces formules. On pourra aussi utiliser le tableur pour vérifier l'exactitude des formules en créant une nouvelle feuille les utilisant pour remplir la colonne donnant le montant de la cagnotte.

  2. Graphiques de déplacements

    3. La plupart des exercices concernant les graphiques consistent à les dessiner à partir d'un tableau de données ou à les interpréter. Le tableur va nous permettre d'introduire un nouveau type d'exercices : un graphique étant donné, retrouver le tableau de données qui permet de l'obtenir.

    La situation proposée

    Il s'agit de représenter graphiquement les déplacements d'une personne entre 8h et 12h. Pour cela on utilise une feuille de calcul sur laquelle on inscrira les heures de quart d'heure en quart d'heure sur la première colonne et la distance séparant le personnage de son point de départ sur la deuxième colonne.
    Heures Distances
    8h  
    8h15  
    8h30  
    8h45  
    9h  
    9h15  
    9h30  
    9h45  
    10h  
    10h15  
    10h30  
    10h45  
    11h  
    11h15  
    11h30  
    11h45  
    12h  
    La colonne des heures sera remplie une fois pour toutes. Le travail à effectuer consistera à remplir la colonne des distances, puis à observer le graphique obtenu à partir des deux colonnes.

    Première question

    Le personnage s'est rendu dans une ville située à 240 km de chez lui. Le graphique représentant son déplacement est un segment de droite. Compléter la colonne des distances et vérifier en affichant le graphique correspondant.

    Note : si les élèves souhaitent effectuer des calculs, ce qui est d'ailleurs souhaitable, ils peuvent utiliser le tableur en écrivant l'opération précédée du signe = dans une cellule qui ne fait pas partie du tableau; le tableur peut aussi servir de calculette.

    Lorsque tout le monde a réussi à obtenir le graphique demandé, on peut changer la distance parcourue et surtout envisager le problème du retour.

    Ajouter une petite pause

    Un trajet de quatre heures s'en s'arrêter n'étant pas recommandé par la Sécurité Routière, notre personnage décide de s'arrêter pendant une demi heure après 2h de route. Cela ne l'empêche pas d'arriver à destination à 12h.

    Comment a-t-il fait ? Construire le graphique correspondant.

    D'autres graphiques

    Dans cette dernière partie de l'activité, le professeur dessine des graphiques au tableau et les élèves doivent les reproduire en utilisant toujours le tableur. Ils pourront aussi utiliser une troisième colonne pour introduire des commentaires racontant l'histoire du trajet.

    Voici quelques exemples de graphiques proposés :

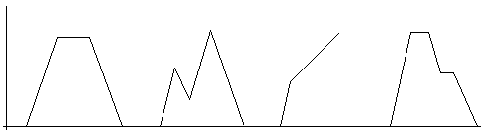
    Cette partie de l'activité laisse une grande part d'initiative aux élèves. La contrainte consistant à fixer le départ à 8h et l'arrivée à 12h les amène à effectuer des calculs répondant aux questions qu'ils se seront posées eux-mêmes.
Voir aussi :