Commencer avec GEOLAP

Avant de se lancer dans des constructions ambitieuses il est bon de se familiariser avec les idées mises en oeuvre dans Geolap sur quelques exemples élémentaires.

  1. Pseudo-cube

    2. Il s'agit de réaliser le dessin des douze arêtes d'un cube en ne décrivant que quatre des ses faces, ce qui est bien suffisant !

    Réalisation d'un carré

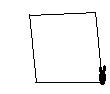    Comme la réalisation d'un carré opération sera répétée plusieurs fois, on définit une instruction supplémentaire : 
    
pour carré (répète 4 (av 60 tg 90)).
    Il suffit donc d'appeler l'instruction carré pour obtenir la figure. Le lapin revient à sa position initiale, dans sa posture de départ.

    Dessin de la seconde face

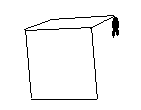    Pour dessiner une seconde face, il est nécessaire de changer de plan, ce qui implique : avancer d'un côté puis piquer de 90°.
    Cela s'obtient avec les instructions : 
    
av 60 pq 90
    On obtient la seconde face en appelant à nouveau l'instruction : 
    
carré.

    Dessin de la troisième face

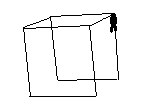    On répète les opérations effectuées pour la seconde face : 
    
;Changement de plan
av 60 pq 90
;Dessin du carré
carré
    Le lapin conserve les position et posture précédentes.

    Dessin de la quatrième face

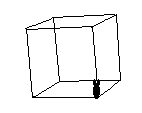    On répète une nouvelle fois les mêmes opérations : 
    
;Changement de plan : 
av 60 pq 90
;Dessin du carré :
carré

    Programme obtenu

    Finalement, en tenant compte des répétitions, on obtient le programme suivant : 
    
pour carré (répète 4 (av 60 tg 90))
répète 4 ( carré av 60 pq 90 )

  2. Le pli entre les faces des solides développables

    3. Un solide réalisé à partir de son développement est dessiné dans le plan, donc avec des faces respectant leurs propriétés géométriques. Mais pour donner sa forme à l'objet, il convient de respecter une mesure précise d'angle dièdre. Il s'agit d'un banal 90° dans le cas du cube ou du pavé droit (ce qui justifie l'utilisation du PQ 90 dans le paragraphe précédent), mais dans la plupart des autres cas, il est plus judicieux de lui substituer un pli "latéral" réalisé par IG ou ID plutôt que le pli "frontal" du PQ.
    A titre d'exemple, nous construirons un "anneau" constitué par la succession de six hexagones réguliers.

    Réalisation d'un hexagone régulier

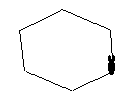
    On définit l'instruction hexagone : 
    
pour hexa (répète 6 (av 70 tg 60 ))
    (observer que le lapin trace l'hexagone en tournant à gauche)

    Face suivante

    
;On plie :
id 60
;On se décale pour passer à la page suivante :
td 120 av 70 tg 60 av 70 tg 60

    Reprendre

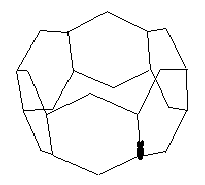    À la fin le lapin revient à sa position de départ.

    Programme obtenu

    
pour hexa (répète 6 (av 70 tg 60))
répète 6 
  (hexa id 60 td 120 av 70 tg 60 av 70 tg 60 )
    À partir de cette simple procédure, il est possible de faire découvrir la valeur correcte du pli en faisant varier la valeur du ID à partir de zéro (un pas de 10 peut suffire mais pourquoi ne pas adopter un pas de 8 qui ne permet pas de refermer de manière satisfaisante ? ).

  3. Patrons de prismes droits

    4. Geolap permet de construire des patrons de solides et bien sûr de les plier et déplier. Pour obtenir le dessin plat du patron il suffit d'utiliser les primitives communes au lapin et à la tortue Logo (av, re, td, tg). Il faudra ensuite gérer les plis en déclarant une ou des variables pli et en indiquant dans le script l'emplacement de ces plis et les changements de plan associés (instructions ig, id, pq, ca).
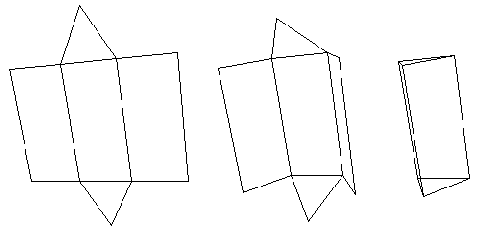
    A titre d'exemple nous construirons un patron de cube et un patron de prisme droit à base triangulaire.

    Un patron de cube

    Il s'agit de réaliser le patron classique d'un cube (en forme de croix). Il y aura ainsi 6 carrés à dessiner et 5 plis à prendre en compte.

    Dessin du patron
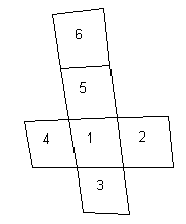    Pour dessiner le patron nous introduirons une constante cot donnant le côté du carré et une procédure carré. 
    
dans cot 100
pour carré 
 (répète 4 (av cot tg 90))
    On dessine ensuite les 6 carrés dans l'ordre indiqué par la figure ci-contre.
    Pour permettre la gestion des plis, on veille à ce que le premier côté d'un des carrés 2 à 6 soit toujours un pli. En tenant compte du fait que les carrés sont construits en tournant vers la gauche, on obtient le script suivant : 
    
dans cot 100
pour carré 
 (répète 4 (av cot tg 90))
;carré 1
carré
;carré 2
lc av cot td 180 bc carré 
;carré 3
lc av cot td 90 bc carré 
;carré 4
lc av cot td 90 bc carré 
;carré 5
lc av cot td 90 bc carré
;carré 6
lc tg 90 av cot td 90 bc carré
    Le patron du cube étant dessiné correctement à la manière de la tortue Logo, il reste à introduire les plis.

    Introduction des plis
    Comme la valeur maximale de chaque pli est 90°, il suffira d'introduire une seule variable pli par l'instruction : 
    
pli a 90
    Ensuite, pour chacun des carrés 2 à 4, on inclinera le lapin de a°, on le tracera et on rétablira enfin la posture du lapin en l'incinant de a° dans l'autre sens. Pour le carré 5 on n'annulera pas cette inclinaison car elle devra être répercutée sur le carré 6.
    Ceci nous donne le script suivant : 
    
pli a 90
dans cot 100
pour carré 
 (répète 4 (av cot tg 90))
;carré 1
carré
;carré 2
lc av cot td 180 bc ig a carré id a
;carré 3
lc av cot td 90 bc ig a carré id a
;carré 4
lc av cot td 90 bc ig a carré id a
;carré 5
lc av cot td 90 bc ig a carré 
;carré 6
lc tg 90 av cot td 90 bc ig a carré
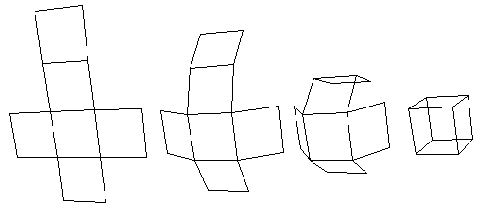
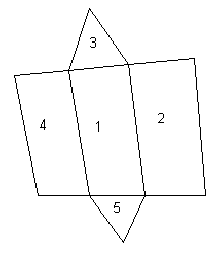
    Ce script permet d'obtenir les figures suivantes :

    Patron d'un prisme droit à base triangulaire

    Nous utiliserons la même démarche que précédemment pour obtenir le patron d'un prisme droit dont la base est un triangle équilatéral. Cette fois deux variables pli interviendront : pli entre deux faces rectangulaires (120°) et pli entre une face rectangulaire et une base (90°).

    Dessin du patron
    Le point de départ sera le dessin classique d'un patron de prisme droit. Pour le réaliser nous définirons des constantes cot et hauteur représentant les longueurs des arêtes et deux procédures triangle et rectangle.
    Lors de l'écriture du script, il faudra, avant de tracer un triangle ou un rectangle, veiller à positionner correctement le lapin pour que le premier côté tracé soit toujours un pli.
    On obtient la figure ci-dessus en utilisant le script : 
    
dans côté 120
dans hauteur 250
pour triangle 
 (répète 3 (av côté tg 120))
pour rectangle 
 (répète 2 (av hauteur tg 90 av côté tg 90))
;face 1
rectangle
;face 2
lc av hauteur tg 180 bc rectangle
;face 3
lc tg 90 re côté bc triangle
;face 4
lc tg 90 re hauteur bc rectangle
;face 5
lc tg 90 re côté bc triangle


    Introduction des plis
    Commençons par définir deux variables pli avec les instructions : 
    
pli a1 120 
pli a2 90
    Il suffit alors d'introduire le pli a1 avant les dessins des rectangles 2 et 4 et le pli a2 avant les dessins des triangles 3 et 5. Comme pour l'exemple précédent du cube, il faudra annuler l'inclinaison induite par le pli après avoir tracé les faces 2 à 5 pour revenir dans le plan de la face 1.
    On obtient finalement le script suivant : 
    
dans côté 120
dans hauteur 250
pli a1 120
pli a2 90
pour triangle 
 (répète 3 (av côté tg 120))
pour rectangle 
 (répète 2 (av hauteur tg 90 av côté tg 90))
;face 1
rectangle
;face 2
lc av hauteur tg 180 bc id a1 rectangle ig a1
;face 3
lc tg 90 re côté bc id a2 triangle ig a2
;face 4
lc tg 90 re hauteur bc id a1 rectangle ig a1
;face 5
lc tg 90 re côté bc id a2 triangle
    On pourra alors observer les étapes suivantes de la construction du prisme droit :

Voir aussi :